Numerisk beräkning av den elektriska
potentialen och det elektriska fältet

För att beräkna potentialen och det elektriska fältet numeriskt används den så kallade fempunktsformeln. (Testladdningarnas rörelse i det elektriska fältet beräknas med Heuns metod vilken beskrivs här.)

Den elektriska potentialen V(x,y) beror av den elektriska laddningsfördelningen r(x,y) i det två-dimensionella rummet med koordinaterna (x,y). Matematiskt ges sambandet mellan potentialen och laddningsfördelningen av följande partiella differential ekvation kallad Poissons ekvation,

d2V(x,y)/dx2 + d2V(x,y)/dy2 = r(x,y)

där d2V(x,y)/dx2 betecknar andra derivatan av potenialen med avseende på x. Om laddningstätheten r(x,y) är noll får vi istället Laplace ekvation vilken är lättare att lösa.

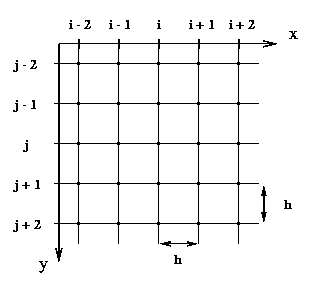
För att lösa Laplace ekvation numeriskt delar vi först in det två dimensionella rummet (x,y) i ett nät av punkter jämnt fördelade i x- och y-led på avståndet h från varandra.

Grid
Potentialens värde i dessa punkter V(xi,yj) används sedan som en approximation till den sanna lösningen V(x,y). Utifrån potentialens värde i punkt nätet kan andraderivatan av potentialen med avseende på x kan approximeras med

d2V(xi,yj)/dx2 = ( V(xi+1,yj) + V(xi-1,yj) - 2*V(xi,yj) ) /h2 .
På samma sätt fås
d2V(xi,yj)/dy2 = ( V(xi,yj+1) + V(xi,yj-1) - 2*V(xi,yj) ) /h2 .

Vilket ger följande approximation till Laplace ekvation,

( V(xi+1,yj) + V(xi-1,yj) + V(xi,yj+1) + V(xi,yj-1) - 4*V(xi,yj) ) /h2 = 0 .

Med andra ord ges potentialen i en punkt V(xi,yj) av medelvärdet av potentialen i de närmaste fyra punkterna,

V(xi,yj) = ( V(xi+1,yj) + V(xi-1,yj) + V(xi,yj+1) + V(xi,yj-1) ) /4 .

Vilket kan illustreras på följande sett.

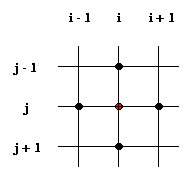
Fempunktsformeln
Av detta följer att om potentialen är känd i någon punkt i rummet så kan den beräknas i alla andra punkter med hjälp av formeln ovan. Genom att applicera formeln ett upprepat antal gånger för varje punkt i rummet så får vi efterhand en bättre och bättre lösning.

Som startfördelning använder vi approximationen att V(xi,yj) = r(xi,yj). I de punkter där r är skild från noll är V konstant medan i övriga punkter så itereras lösning till V fram på det sätt som beskrivs ovan. När skillnaden mellan den nya och gamla lösningen är tillräckligt liten så att önskad precision uppnåtts är beräkningen färdig.

Numerisk beräkning av det elektriska fältet

Det elektriska fältet ges av gradienten av den elektriska potenialen,

E(x,y) = - (dV(x,y)/dx , dV(x,y)/dy)

Observera att det elektriska fältet är ett vektor fält med två komponenter (värden), en i x-led och en i y-led, E(x,y)=(Ex(x,y),Ey(x,y)). Numeriskt kan det elektriska fältets två komponenter approximeras med,

Ex(xi,yj) = - [ V(xi+1,yj) - V(xi-1,yj) ] /(2*h)
Ey(xi,yj) = - [ V(xi,yj+1) - V(xi,yj-1) ] /(2*h)

Det finns ännu noggrannare approximationer för att beräkna potentialen och det elektriska fältet.

Den Java-kod som räknar ut potentialen och det elektriska fältet finns här.