Teori för Ising modellen

Isingmodellen är en modell för hur de magnetiska spinnen hos atomerna i ett ferromagnetiskt material växelverkar med varandra.

Spinn är en kvantmekanisk egenskap hos partiklar som inte lätt låter sig förklaras i klassiska termer. För att förstå Isingmodellen kan man tänka på spinn som att varje atom är en liten magnet som endast kan peka åt två håll, uppåt eller nedåt. Spinnet, s är ett tal som anger vilken riktning magneten pekar åt, +1 för uppåt och -1 för nedåt. Medan styrkan på magneten ges av det magnetisk momentet, mu.

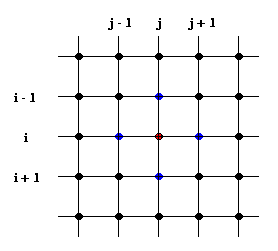
I den två-dimensionella Isingmodellen antas atomerna vara ordnade i ett gitter (rutnät) med en atom på varje position. Positionerna betecknas med två nummer, i,j där det första anger raden och det andra kolumnen.

Varje atom växelverkar dels med det yttre pålagda magnetiska fältet, H och dels med sina fyra närmaste grannar. Med andra ord, atomen markerat med rött i figuren växelverkar med de fyra atomer som är markerade med blått. Energin för en atom i position i,j ges då av,

E_i,j = - H*mu*s_i,j - 0.5*J*s_i,j*( s_i+1,j + s_i-1,j + s_i,j+1 + s_i,j-1)

där J anger hur stark kopplingen är mellan spinnen hos två närliggande atomer. (Faktorn 0.5 är en symmetri faktor som uppstår om man summerar över alla atomer istället för över alla par av närmaste grannar.) Den totala energin fås genom att ta summan av energin för alla atomer.

De atomer som sitter längs kanten på gittret måste behandlas på ett särskilt sätt eftersom de inte har grannar på alla sidor. Detta löses genom att applicera så kallade periodiska randvillkor. Det innebär att atomerna på den högra kanten antas ha atomerna på den vänstra kanten som grannar till höger och vice versa. På samma sätt antas över- och underkanten ligga intill varandra.

För att simulera hur atomerna beter sig så används så kallad Monte Carlo simulering. Det går till så att man startar från ett tillstånd där varje atom har fått ett slumpmässigt valt spinn. (I programmet görs detta genom att trycka på knappen "Blanda".) Därefter gäller det att försöka komma fram till ett jämviktstillstånd. Detta sker genom en stegvis procedur. Efter tillräckligt många steg når man så småningom ett jämviktstillstånd.

I varje steg väljer man först slumpmässigt ut en av atomerna i gittret och beräknar energin för hela tillståndet. Energin beräknas både för det spinn atomen har, E_gammal, och motsatt spinn, E_ny. Om E_ny är mindre än E_gammal så byts spinnet på atomen eftersom den totala energin blir lägre. Om däremot E_ny är större än E_gammal så byts spinnet med sannolikheten

P = exp( (E_gammal - E_ny) / (k*T) )

där k är Boltzmans konstant^* och T är temperaturen. Det finns alltså en möjlighet att spinnet hos en atom ändras även fast det ökar energin. Av formeln för sannolikheten för att spinnet ska bytas ser man att ju större skillnaden i energi är desto mindre är sannolikheten för att spinnet ska ändras. Man ser också att vid högre temperaturer så är sannolikheten större för att spinnet ska ändras. Med andra ord är det två konkurrerande processer som pågar parallellt. Dels så finns det en strävan att minimera den totala energin för systemet och dels så finns det störningar som gör att en atom kan byta spinn trots att det ökar energin.

Då ett jämviktstillstånd har uppnåtts kan energin och magnetiseringen bestämmas. Magnetiseringen ges av summan av alla spinn gånger det magnetiska momentet. Med andra ord ges bidraget till magnetiseringen från en atom av

M_i,j = mu*s_i,j

och den totala magnetiseringen fås genom att summera över alla atomer. På samma sätt ges den totala energin av summan av energin för alla atomer. För att få en bättre uppskattning av värdet på magnetiseringen och energin kan man ta medelvärdet av flera olika jämviktstillstånd och från de statistiska fluktuationerna kan man uppskatta felet.

^* För att göra formlerna så enkla som möjligt har enheterna valts så att Boltzmanns konstant har värdet k=1. Detta innebär att till exempel att energin mäts i samma enhet som temperaturen, dvs i Kelvin.