Kendall's tau rank coefficient. More...

#include <yat/statistics/Kendall.h>

Public Member Functions
	Kendall (void)
	Constructor.

	Kendall (const Kendall &other)
	Copy constructor.

virtual	~Kendall (void)
	Destructor.

void	add (double x, double y)
	add pair of data

size_t	n (void) const

double	p_left (bool exact=false) const
	Lower one-sided p-value. More...

double	p_right (bool exact=false) const
	Upper one-sided p-value. More...

double	p_value (bool exact=false) const
	Two-sided p-value.

void	reset (void)
	reset

double	score (void) const
	Kendall's tau. More...

Kendall &	operator= (const Kendall &rhs)
	assignment operator

Detailed Description

Kendall's tau rank coefficient.

Member Function Documentation

size_t theplu::yat::statistics::Kendall::n ( void ) const

Returns: Number of data points

double theplu::yat::statistics::Kendall::p_left ( bool exact = false ) const

Lower one-sided p-value.

P-value is calculates in same fashion as p_right(), but calculating when score from permuted data is smaller than score (rather than greater).

See Also: p_right()

double theplu::yat::statistics::Kendall::p_right ( bool exact = false ) const

Upper one-sided p-value.

If exact function permutaes the data and counts fraction of permutations that result in a larger tau coefficient.

If not exact a Gaussian approximation by transforming the score to a variable a z is approximately stardard normal, where

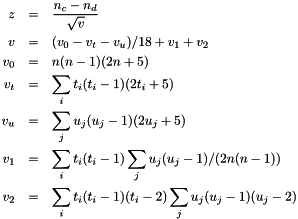
$\begin{eqnarray*} z &=& \frac{n_c - n_d}{\sqrt{v}} \\ v &=& (v_0-v_t-v_u)/18+v_1+v_2 \\ v_0 &=& n(n-1)(2n+5) \\ v_t &=& \sum_i t_i(t_i-1)(2t_i+5) \\ v_u &=& \sum_j u_j(u_j-1)(2u_j+5) \\ v_1 &=& \sum_i t_i(t_i-1)\sum_j u_j(u_j-1)/(2n(n-1)) \\ v_2 &=& \sum_i t_i(t_i-1)(t_i-2)\sum_j u_j(u_j-1)(u_j-2) \end{eqnarray*}$

(see function score() for explanation of variables).

and p-value is calculates as 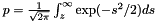$p = \frac{1}{\sqrt{2\pi}} \int_z^{\infty} \exp(-s^2/2) ds$

double theplu::yat::statistics::Kendall::score ( void ) const

Kendall's tau.

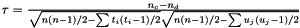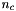$\tau = \frac{n_c - n_d}{\sqrt{n(n-1)/2-\sum t_i(t_i-1)/2}\sqrt{n(n-1)/2-\sum u_j(u_j-1)/2}}$ where $ n_c $ is number concordant pairs, 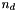$ n_d $ number of disconcordant pairs, 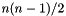$ n(n-1)/2 $ total number of pairs, 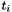$ t_i $ number of data points in ties group i, and 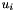$ u_i $ number of data points in tied group j

The documentation for this class was generated from the following file:

yat/statistics/Kendall.h

Public Member Functions

Detailed Description

Member Function Documentation