Kolmogorov Smirnov Test for one class. More...

#include <yat/statistics/KolmogorovSmirnovOneSample.h>

Public Member Functions
	KolmogorovSmirnovOneSample (void)
	Constructor.

void	add (double value, double weight=1.0)
	add a value More...

double	p_value (void) const
	Large-Sample Approximation. More...

void	remove (double value, double weight=1.0)
	Remove a data point. More...

void	reset (void)
	resets everything to zero

double	score (void) const
	Kolmogorov Smirnov statistic. More...

double	signed_score (void) const

Friends
std::ostream &	operator<< (std::ostream &, const KolmogorovSmirnovOneSample &)

Detailed Description

Kolmogorov Smirnov Test for one class.

Class can be used to test if data follows standard uniform distribution. Other distributions are not supported directly, but it is possible to check against other distribution by tranforming the data. If, for example, X is standard exponentially distributed log(X) is standard uniform. Therefore, rather than testing if X is exponential it is equivalent to test if log(X) is standard uniform.

Since: New in yat 0.11

Member Function Documentation

void theplu::yat::statistics::KolmogorovSmirnovOneSample::add	(	double	value,
		double	weight = `1.0`
	)

add a value

value should be a value in range [0, 1].

double theplu::yat::statistics::KolmogorovSmirnovOneSample::p_value ( void ) const

Large-Sample Approximation.

This analytical approximation of p-value can be used when all weight equal unity and sample size n is large. The p-value is calcuated as 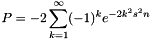$P = \displaystyle - 2 \sum_{k=1}^{\infty} (-1)^ke^{-2k^2s^2n}$ , where s is the score and n is the sum of weights.

void theplu::yat::statistics::KolmogorovSmirnovOneSample::remove	(	double	value,
		double	weight = `1.0`
	)

Remove a data point.

Exceptions

utility::runtime_error if no data point exist with value and weight.

double theplu::yat::statistics::KolmogorovSmirnovOneSample::score ( void ) const

Kolmogorov Smirnov statistic.

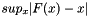$ sup_x | F(x) - x | $ where is the empirical cumulative distribution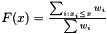 $F(x) = \frac{\sum_{i:x_i\le x}w_i}{ \sum w_i}$

double theplu::yat::statistics::KolmogorovSmirnovOneSample::signed_score ( void ) const

Same as score() but keeping the sign, in other words, abs(signed_score())==score()

A positive score implies that values on average are smaller 0.5.

The documentation for this class was generated from the following file:

yat/statistics/KolmogorovSmirnovOneSample.h

Public Member Functions

Friends

Detailed Description

Member Function Documentation