Spearman rank correlation coefficient. More...
#include <yat/statistics/Spearman.h>
Public Member Functions | |
| Spearman (void) | |
| Constructor. | |
| virtual | ~Spearman (void) |
| Destructor. | |
| void | add (double x, double y) |
| add pair of data | |
| size_t | n (void) const |
| Number of data points. More... | |
| double | p_left (bool exact=false) const |
| Lower one-sided p-value. More... | |
| double | p_right (bool exact=false) const |
| Upper one-sided p-value. More... | |
| double | p_value (bool exact=false) const |
| Two-sided p-value. More... | |
| void | reset (void) |
| reset to empty | |
| double | score (void) const |
| spearman rank correlation coefficient More... | |
Detailed Description
Spearman rank correlation coefficient.
Class for Spearman rank correlation coefficient which can be understood as Pearson correlation of ranks.
- Since
- New in yat 0.9
Member Function Documentation
| size_t theplu::yat::statistics::Spearman::n | ( | void | ) | const |
Number of data points.
- Returns
- Number of pairs of data added to object.
| double theplu::yat::statistics::Spearman::p_left | ( | bool | exact = false | ) | const |
| double theplu::yat::statistics::Spearman::p_right | ( | bool | exact = false | ) | const |
Upper one-sided p-value.
Calculates, 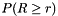 , the probability to get a score greater (or equal) than score() given that there is no association between two variables.
, the probability to get a score greater (or equal) than score() given that there is no association between two variables.
In exact mode the score is calculated for each permutation and compared to the actual score. In each permutation one variable, say x, is kept fix while the other (y) is shuffled in determionsitic fashion. Number of permutations grows quickly as number of data points grows and with no ties there are N! permutations and the exact method gets very expensive.
In approximative mode P-value is calculated using pearson_p_value().
| double theplu::yat::statistics::Spearman::p_value | ( | bool | exact = false | ) | const |
| double theplu::yat::statistics::Spearman::score | ( | void | ) | const |
spearman rank correlation coefficient
The Spearman rank correlation coeeficient is defined as 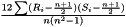 where
where 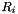 and
and 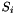 are ranks of X and Y, respectively. In case of ties, the rank is defined as the average rank of the ties.
are ranks of X and Y, respectively. In case of ties, the rank is defined as the average rank of the ties.
The documentation for this class was generated from the following file:
- yat/statistics/Spearman.h
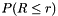 , the probability to get a score less (or equal) than
, the probability to get a score less (or equal) than 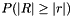 , the probability to get a score more extreme (or equal) than
, the probability to get a score more extreme (or equal) than  1.8.5
1.8.5