Class for Student's t-test. More...

#include <yat/statistics/tTest.h>

Public Member Functions
	tTest (void)
	Default Constructor.

void	add (double value, bool target, double weight=1.0)

void	reset (void)
	Set everything to zero. More...

double	score (void) const

double	p_left (void) const

double	p_right (void) const

double	p_value () const

double	p_value_one_sided (void) const

Detailed Description

Class for Student's t-test.

See http://en.wikipedia.org/wiki/Student's_t-test for more details on the t-test.

Member Function Documentation

void theplu::yat::statistics::tTest::add	(	double	value,
		bool	target,
		double	weight = `1.0`
	)

Adding a data value to tTest.

double theplu::yat::statistics::tTest::p_left ( void ) const

Returns: the probability of observing a t-score that is equal or smaller than score().

double theplu::yat::statistics::tTest::p_right ( void ) const

Returns: the one-sided p-value, i.e., the probability of observing a t-score that is equal or greater than observed here.

double theplu::yat::statistics::tTest::p_value ( ) const

Calculates the two-sided p-value, i.e., the probability to observe a t-score equal (or greater) than |t| or smaller than -|t|, where t is the observed t-score (returned by score()).

Returns: the two-sided p-value

double theplu::yat::statistics::tTest::p_value_one_sided ( void ) const

Deprecated:: Provided for backward compatibility with 0.10 API. Use p_right() instead.

void theplu::yat::statistics::tTest::reset ( void )

Set everything to zero.

Since: New in yat 0.5

double theplu::yat::statistics::tTest::score ( void ) const

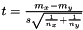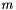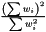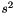Calculates the t-score, i.e. the ratio between difference in mean and standard deviation of this difference. The t-score is calculated as $t = \frac{ m_x - m_y }{ s\sqrt{\frac{1}{n_x}+\frac{1}{n_y}}}$ where $ m $ is the weighted mean, n is the weighted version of number of data points $\frac{\left(\sum w_i\right)^2}{\sum w_i^2}$ , and $ s^2 $ is an estimation of the variance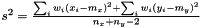 $s^2 = \frac{ \sum_i w_i(x_i-m_x)^2 + \sum_i w_i(y_i-m_y)^2 }{ n_x + n_y - 2 }$

See Also: AveragerWeighted

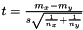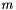If all weights are equal to unity this boils down to $t = \frac{ m_x - m_y } {s\sqrt{\frac{1}{n_x}+\frac{1}{n_y}}}$ where $ m $ is the mean, 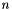$ n $ is the number of data points and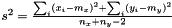 $s^2 = \frac{ \sum_i (x_i-m_x)^2 + \sum_i (y_i-m_y)^2 }{ n_x + n_y - 2 }$

See Also: Averager

Returns: t-score.

The documentation for this class was generated from the following file:

yat/statistics/tTest.h

Public Member Functions

Detailed Description

Member Function Documentation