ThePEG::ParticleID Namespace Reference

The ParticleID namespace defines the ParticleCodes enumeration. More...


Enumerations

enum  ParticleCodes {
  d = 1, dbar = -1, u = 2, ubar = -2,
  s = 3, sbar = -3, c = 4, cbar = -4,
  b = 5, bbar = -5, t = 6, tbar = -6,
  bprime = 7, bprimebar = -7, tprime = 8, tprimebar = -8,
  eminus = 11, eplus = -11, nu_e = 12, nu_ebar = -12,
  muminus = 13, muplus = -13, nu_mu = 14, nu_mubar = -14,
  tauminus = 15, tauplus = -15, nu_tau = 16, nu_taubar = -16,
  tauprimeminus = 17, tauprimeplus = -17, nuprime_tau = 18, nuprime_taubar = -18,
  g = 21, gamma = 22, Z0 = 23, Wplus = 24,
  Wminus = -24, h0 = 25, Zprime0 = 32, Zbis0 = 33,
  Wprimeplus = 34, Wprimeminus = -34, H0 = 35, A0 = 36,
  Hplus = 37, Hminus = -37, Graviton = 39, R0 = 41,
  Rbar0 = -41, LQ_ue = 42, LQ_uebar = -42, reggeon = 110,
  pi0 = 111, rho0 = 113, a_20 = 115, K_L0 = 130,
  piplus = 211, piminus = -211, rhoplus = 213, rhominus = -213,
  a_2plus = 215, a_2minus = -215, eta = 221, omega = 223,
  f_2 = 225, K_S0 = 310, K0 = 311, Kbar0 = -311,
  Kstar0 = 313, Kstarbar0 = -313, Kstar_20 = 315, Kstar_2bar0 = -315,
  Kplus = 321, Kminus = -321, Kstarplus = 323, Kstarminus = -323,
  Kstar_2plus = 325, Kstar_2minus = -325, etaprime = 331, phi = 333,
  fprime_2 = 335, Dplus = 411, Dminus = -411, Dstarplus = 413,
  Dstarminus = -413, Dstar_2plus = 415, Dstar_2minus = -415, D0 = 421,
  Dbar0 = -421, Dstar0 = 423, Dstarbar0 = -423, Dstar_20 = 425,
  Dstar_2bar0 = -425, D_splus = 431, D_sminus = -431, Dstar_splus = 433,
  Dstar_sminus = -433, Dstar_2splus = 435, Dstar_2sminus = -435, eta_c = 441,
  Jpsi = 443, chi_2c = 445, B0 = 511, Bbar0 = -511,
  Bstar0 = 513, Bstarbar0 = -513, Bstar_20 = 515, Bstar_2bar0 = -515,
  Bplus = 521, Bminus = -521, Bstarplus = 523, Bstarminus = -523,
  Bstar_2plus = 525, Bstar_2minus = -525, B_s0 = 531, B_sbar0 = -531,
  Bstar_s0 = 533, Bstar_sbar0 = -533, Bstar_2s0 = 535, Bstar_2sbar0 = -535,
  B_cplus = 541, B_cminus = -541, Bstar_cplus = 543, Bstar_cminus = -543,
  Bstar_2cplus = 545, Bstar_2cminus = -545, eta_b = 551, Upsilon = 553,
  chi_2b = 555, pomeron = 990, dd_1 = 1103, dd_1bar = -1103,
  Deltaminus = 1114, Deltabarplus = -1114, ud_0 = 2101, ud_0bar = -2101,
  ud_1 = 2103, ud_1bar = -2103, n0 = 2112, nbar0 = -2112,
  Delta0 = 2114, Deltabar0 = -2114, uu_1 = 2203, uu_1bar = -2203,
  pplus = 2212, pbarminus = -2212, Deltaplus = 2214, Deltabarminus = -2214,
  Deltaplus2 = 2224, Deltabarminus2 = -2224, sd_0 = 3101, sd_0bar = -3101,
  sd_1 = 3103, sd_1bar = -3103, Sigmaminus = 3112, Sigmabarplus = -3112,
  Sigmastarminus = 3114, Sigmastarbarplus = -3114, Lambda0 = 3122, Lambdabar0 = -3122,
  su_0 = 3201, su_0bar = -3201, su_1 = 3203, su_1bar = -3203,
  Sigma0 = 3212, Sigmabar0 = -3212, Sigmastar0 = 3214, Sigmastarbar0 = -3214,
  Sigmaplus = 3222, Sigmabarminus = -3222, Sigmastarplus = 3224, Sigmastarbarminus = -3224,
  ss_1 = 3303, ss_1bar = -3303, Ximinus = 3312, Xibarplus = -3312,
  Xistarminus = 3314, Xistarbarplus = -3314, Xi0 = 3322, Xibar0 = -3322,
  Xistar0 = 3324, Xistarbar0 = -3324, Omegaminus = 3334, Omegabarplus = -3334,
  cd_0 = 4101, cd_0bar = -4101, cd_1 = 4103, cd_1bar = -4103,
  Sigma_c0 = 4112, Sigma_cbar0 = -4112, Sigmastar_c0 = 4114, Sigmastar_cbar0 = -4114,
  Lambda_cplus = 4122, Lambda_cbarminus = -4122, Xi_c0 = 4132, Xi_cbar0 = -4132,
  cu_0 = 4201, cu_0bar = -4201, cu_1 = 4203, cu_1bar = -4203,
  Sigma_cplus = 4212, Sigma_cbarminus = -4212, Sigmastar_cplus = 4214, Sigmastar_cbarminus = -4214,
  Sigma_cplus2 = 4222, Sigma_cbarminus2 = -4222, Sigmastar_cplus2 = 4224, Sigmastar_cbarminus2 = -4224,
  Xi_cplus = 4232, Xi_cbarminus = -4232, cs_0 = 4301, cs_0bar = -4301,
  cs_1 = 4303, cs_1bar = -4303, Xiprime_c0 = 4312, Xiprime_cbar0 = -4312,
  Xistar_c0 = 4314, Xistar_cbar0 = -4314, Xiprime_cplus = 4322, Xiprime_cbarminus = -4322,
  Xistar_cplus = 4324, Xistar_cbarminus = -4324, Omega_c0 = 4332, Omega_cbar0 = -4332,
  Omegastar_c0 = 4334, Omegastar_cbar0 = -4334, cc_1 = 4403, cc_1bar = -4403,
  Xi_ccplus = 4412, Xi_ccbarminus = -4412, Xistar_ccplus = 4414, Xistar_ccbarminus = -4414,
  Xi_ccplus2 = 4422, Xi_ccbarminus2 = -4422, Xistar_ccplus2 = 4424, Xistar_ccbarminus2 = -4424,
  Omega_ccplus = 4432, Omega_ccbarminus = -4432, Omegastar_ccplus = 4434, Omegastar_ccbarminus = -4434,
  Omegastar_cccplus2 = 4444, Omegastar_cccbarminus = -4444, bd_0 = 5101, bd_0bar = -5101,
  bd_1 = 5103, bd_1bar = -5103, Sigma_bminus = 5112, Sigma_bbarplus = -5112,
  Sigmastar_bminus = 5114, Sigmastar_bbarplus = -5114, Lambda_b0 = 5122, Lambda_bbar0 = -5122,
  Xi_bminus = 5132, Xi_bbarplus = -5132, Xi_bc0 = 5142, Xi_bcbar0 = -5142,
  bu_0 = 5201, bu_0bar = -5201, bu_1 = 5203, bu_1bar = -5203,
  Sigma_b0 = 5212, Sigma_bbar0 = -5212, Sigmastar_b0 = 5214, Sigmastar_bbar0 = -5214,
  Sigma_bplus = 5222, Sigma_bbarminus = -5222, Sigmastar_bplus = 5224, Sigmastar_bbarminus = -5224,
  Xi_b0 = 5232, Xi_bbar0 = -5232, Xi_bcplus = 5242, Xi_bcbarminus = -5242,
  bs_0 = 5301, bs_0bar = -5301, bs_1 = 5303, bs_1bar = -5303,
  Xiprime_bminus = 5312, Xiprime_bbarplus = -5312, Xistar_bminus = 5314, Xistar_bbarplus = -5314,
  Xiprime_b0 = 5322, Xiprime_bbar0 = -5322, Xistar_b0 = 5324, Xistar_bbar0 = -5324,
  Omega_bminus = 5332, Omega_bbarplus = -5332, Omegastar_bminus = 5334, Omegastar_bbarplus = -5334,
  Omega_bc0 = 5342, Omega_bcbar0 = -5342, bc_0 = 5401, bc_0bar = -5401,
  bc_1 = 5403, bc_1bar = -5403, Xiprime_bc0 = 5412, Xiprime_bcbar0 = -5412,
  Xistar_bc0 = 5414, Xistar_bcbar0 = -5414, Xiprime_bcplus = 5422, Xiprime_bcbarminus = -5422,
  Xistar_bcplus = 5424, Xistar_bcbarminus = -5424, Omegaprime_bc0 = 5432, Omegaprime_bcba = -5432,
  Omegastar_bc0 = 5434, Omegastar_bcbar0 = -5434, Omega_bccplus = 5442, Omega_bccbarminus = -5442,
  Omegastar_bccplus = 5444, Omegastar_bccbarminus = -5444, bb_1 = 5503, bb_1bar = -5503,
  Xi_bbminus = 5512, Xi_bbbarplus = -5512, Xistar_bbminus = 5514, Xistar_bbbarplus = -5514,
  Xi_bb0 = 5522, Xi_bbbar0 = -5522, Xistar_bb0 = 5524, Xistar_bbbar0 = -5524,
  Omega_bbminus = 5532, Omega_bbbarplus = -5532, Omegastar_bbminus = 5534, Omegastar_bbbarplus = -5534,
  Omega_bbc0 = 5542, Omega_bbcbar0 = -5542, Omegastar_bbc0 = 5544, Omegastar_bbcbar0 = -5544,
  Omegastar_bbbminus = 5554, Omegastar_bbbbarplus = -5554, a_00 = 9000111, b_10 = 10113,
  a_0plus = 9000211, a_0minus = -9000211, b_1plus = 10213, b_1minus = -10213,
  f_0 = 9010221, h_1 = 10223, Kstar_00 = 10311, Kstar_0bar0 = -10311,
  K_10 = 10313, K_1bar0 = -10313, Kstar_0plus = 10321, Kstar_0minus = -10321,
  K_1plus = 10323, K_1minus = -10323, eta1440 = 100331, hprime_1 = 10333,
  Dstar_0plus = 10411, Dstar_0minus = -10411, D_1plus = 10413, D_1minus = -10413,
  Dstar_00 = 10421, Dstar_0bar0 = -10421, D_10 = 10423, D_1bar0 = -10423,
  Dstar_0splus = 10431, Dstar_0sminus = -10431, D_1splus = 10433, D_1sminus = -10433,
  chi_0c = 10441, h_1c = 10443, Bstar_00 = 10511, Bstar_0bar0 = -10511,
  B_10 = 10513, B_1bar0 = -10513, Bstar_0plus = 10521, Bstar_0minus = -10521,
  B_1plus = 10523, B_1minus = -10523, Bstar_0s0 = 10531, Bstar_0sbar0 = -10531,
  B_1s0 = 10533, B_1sbar0 = -10533, Bstar_0cplus = 10541, Bstar_0cminus = -10541,
  B_1cplus = 10543, B_1cminus = -10543, chi_0b = 10551, h_1b = 10553,
  a_10 = 20113, a_1plus = 20213, a_1minus = -20213, f_1 = 20223,
  Kstar_10 = 20313, Kstar_1bar0 = -20313, Kstar_1plus = 20323, Kstar_1minus = -20323,
  fprime_1 = 20333, Dstar_1plus = 20413, Dstar_1minus = -20413, Dstar_10 = 20423,
  Dstar_1bar0 = -20423, Dstar_1splus = 20433, Dstar_1sminus = -20433, chi_1c = 20443,
  Bstar_10 = 20513, Bstar_1bar0 = -20513, Bstar_1plus = 20523, Bstar_1minus = -20523,
  Bstar_1s0 = 20533, Bstar_1sbar0 = -20533, Bstar_1cplus = 20543, Bstar_1cminus = -20543,
  chi_1b = 20553, psiprime = 100443, Upsilonprime = 100553, SUSY_d_L = 1000001,
  SUSY_d_Lbar = -1000001, SUSY_u_L = 1000002, SUSY_u_Lbar = -1000002, SUSY_s_L = 1000003,
  SUSY_s_Lbar = -1000003, SUSY_c_L = 1000004, SUSY_c_Lbar = -1000004, SUSY_b_1 = 1000005,
  SUSY_b_1bar = -1000005, SUSY_t_1 = 1000006, SUSY_t_1bar = -1000006, SUSY_e_Lminus = 1000011,
  SUSY_e_Lplus = -1000011, SUSY_nu_eL = 1000012, SUSY_nu_eLbar = -1000012, SUSY_mu_Lminus = 1000013,
  SUSY_mu_Lplus = -1000013, SUSY_nu_muL = 1000014, SUSY_nu_muLbar = -1000014, SUSY_tau_1minus = 1000015,
  SUSY_tau_1plus = -1000015, SUSY_nu_tauL = 1000016, SUSY_nu_tauLbar = -1000016, SUSY_g = 1000021,
  SUSY_chi_10 = 1000022, SUSY_chi_20 = 1000023, SUSY_chi_1plus = 1000024, SUSY_chi_1minus = -1000024,
  SUSY_chi_30 = 1000025, SUSY_chi_40 = 1000035, SUSY_chi_2plus = 1000037, SUSY_chi_2minus = -1000037,
  SUSY_Gravitino = 1000039, SUSY_d_R = 2000001, SUSY_d_Rbar = -2000001, SUSY_u_R = 2000002,
  SUSY_u_Rbar = -2000002, SUSY_s_R = 2000003, SUSY_s_Rbar = -2000003, SUSY_c_R = 2000004,
  SUSY_c_Rbar = -2000004, SUSY_b_2 = 2000005, SUSY_b_2bar = -2000005, SUSY_t_2 = 2000006,
  SUSY_t_2bar = -2000006, SUSY_e_Rminus = 2000011, SUSY_e_Rplus = -2000011, SUSY_nu_eR = 2000012,
  SUSY_nu_eRbar = -2000012, SUSY_mu_Rminus = 2000013, SUSY_mu_Rplus = -2000013, SUSY_nu_muR = 2000014,
  SUSY_nu_muRbar = -2000014, SUSY_tau_2minus = 2000015, SUSY_tau_2plus = -2000015, SUSY_nu_tauR = 2000016,
  SUSY_nu_tauRbar = -2000016, pi_tc0 = 3000111, pi_tcplus = 3000211, pi_tcminus = -3000211,
  piprime_tc0 = 3000221, eta_tc0 = 3000331, rho_tc0 = 3000113, rho_tcplus = 3000213,
  rho_tcminus = -3000213, omega_tc = 3000223, V8_tc = 3100021, pi_22_1_tc = 3100111,
  pi_22_8_tc = 3200111, rho_11_tc = 3100113, rho_12_tc = 3200113, rho_21_tc = 3300113,
  rho_22_tc = 3400113, dstar = 4000001, dstarbar = -4000001, ustar = 4000002,
  ustarbar = -4000002, estarminus = 4000011, estarbarplus = -4000011, nustar_e0 = 4000012,
  nustar_ebar0 = -4000012, Gravitonstar = 5000039, nu_Re = 9900012, nu_Rmu = 9900014,
  nu_Rtau = 9900016, Z_R0 = 9900023, W_Rplus = 9900024, W_Rminus = -9900024,
  H_Lplus2 = 9900041, H_Lminus2 = -9900041, H_Rplus2 = 9900042, H_Rminus2 = -9900042,
  rho_diff0 = 9900110, pi_diffrplus = 9900210, pi_diffrminus = -9900210, omega_di = 9900220,
  phi_diff = 9900330, Jpsi_di = 9900440, n_diffr0 = 9902110, n_diffrbar0 = -9902110,
  p_diffrplus = 9902210, p_diffrbarminus = -9902210, undefined = 0
}
 Enumeration to give identifiers to PDG id numbers. More...

Detailed Description

The ParticleID namespace defines the ParticleCodes enumeration.

Enumeration Type Documentation

enum ThePEG::ParticleID::ParticleCodes

Enumeration to give identifiers to PDG id numbers.

Enumerator:
d  $\mbox{d}$ (d)
dbar  $\overline{\mbox{d}}$ (dbar)
u  $\mbox{u}$ (u)
ubar  $\overline{\mbox{u}}$ (ubar)
s  $\mbox{s}$ (s)
sbar  $\overline{\mbox{s}}$ (sbar)
c  $\mbox{c}$ (c)
cbar  $\overline{\mbox{c}}$ (cbar)
b  $\mbox{b}$ (b)
bbar  $\overline{\mbox{b}}$ (bbar)
t  $\mbox{t}$ (t)
tbar  $\overline{\mbox{t}}$ (tbar)
bprime  $\mbox{b}^{\prime }$ (b')
bprimebar  $\overline{\mbox{b}}^{\prime }$ (b'bar)
tprime  $\mbox{t}^{\prime }$ (t')
tprimebar  $\overline{\mbox{t}}^{\prime }$ (t'bar)
eminus  $\mbox{e}^{-}$ (e-)
eplus  $\mbox{e}^{+}$ (e+)
nu_e  $\nu _{e}$ (nu_e)
nu_ebar  $\overline{\nu }_{e}$ (nu_ebar)
muminus  $\mu ^{-}$ (mu-)
muplus  $\mu ^{+}$ (mu+)
nu_mu  $\nu _{\mu }$ (nu_mu)
nu_mubar  $\overline{\nu }_{\mu }$ (nu_mubar)
tauminus  $\tau ^{-}$ (tau-)
tauplus  $\tau ^{+}$ (tau+)
nu_tau  $\nu _{\tau }$ (nu_tau)
nu_taubar  $\overline{\nu }_{\tau }$ (nu_taubar)
tauprimeminus  $\tau ^{\prime -}$ (tau'-)
tauprimeplus  $\tau ^{\prime +}$ (tau'+)
nuprime_tau  $\nu ^{\prime }_{\tau }$ (nu'_tau)
nuprime_taubar  $\overline{\nu }^{\prime }_{\tau }$ (nu'_taubar)
g  $\mbox{g}$ (g)
gamma  $\gamma $ (gamma)
Z0  $\mbox{Z}^{0 }$ (Z0)
Wplus  $\mbox{W}^{+}$ (W+)
Wminus  $\mbox{W}^{-}$ (W-)
h0  $\mbox{h}^{0 }$ (h0)
Zprime0  $\mbox{Z}^{\prime 0 }$ (Z'0)
Zbis0  $\mbox{Z}^{\prime\prime 0 }$ (Z"0)
Wprimeplus  $\mbox{W}^{\prime +}$ (W'+)
Wprimeminus  $\mbox{W}^{\prime -}$ (W'-)
H0  $\mbox{H}^{0 }$ (H0)
A0  $\mbox{A}^{0 }$ (A0)
Hplus  $\mbox{H}^{+}$ (H+)
Hminus  $\mbox{H}^{-}$ (H-)
Graviton  ${\cal G}$ (Graviton)
R0  $\mbox{R}^{0 }$ (R0)
Rbar0  $\overline{\mbox{R}}^{0 }$ (Rbar0)
LQ_ue  $\mbox{L}_{Que}$ (LQ_ue)
LQ_uebar  $\overline{\mbox{L}}_{Que}$ (LQ_uebar)
reggeon  $I\!\!R$ (reggeon)
pi0  $\pi ^{0 }$ (pi0)
rho0  $\rho ^{0 }$ (rho0)
a_20  $\mbox{a}^{0 }_{2}$ (a_20)
K_L0  $\mbox{K}^{0 }_{L}$ (K_L0)
piplus  $\pi ^{+}$ (pi+)
piminus  $\pi ^{-}$ (pi-)
rhoplus  $\rho ^{+}$ (rho+)
rhominus  $\rho ^{-}$ (rho-)
a_2plus  $\mbox{a}^{+}_{2}$ (a_2+)
a_2minus  $\mbox{a}^{-}_{2}$ (a_2-)
eta  $\eta $ (eta)
omega  $\omega $ (omega)
f_2  $\mbox{f}_{2}$ (f_2)
K_S0  $\mbox{K}^{0 }_{S}$ (K_S0)
K0  $\mbox{K}^{0 }$ (K0)
Kbar0  $\overline{\mbox{K}}^{0 }$ (Kbar0)
Kstar0  $\mbox{K}^{*0 }$ (K*0)
Kstarbar0  $\overline{\mbox{K}}^{*0 }$ (K*bar0)
Kstar_20  $\mbox{K}^{*0 }_{2}$ (K*_20)
Kstar_2bar0  $\overline{\mbox{K}}^{*0 }_{2}$ (K*_2bar0)
Kplus  $\mbox{K}^{+}$ (K+)
Kminus  $\mbox{K}^{-}$ (K-)
Kstarplus  $\mbox{K}^{*+}$ (K*+)
Kstarminus  $\mbox{K}^{*-}$ (K*-)
Kstar_2plus  $\mbox{K}^{*+}_{2}$ (K*_2+)
Kstar_2minus  $\mbox{K}^{*-}_{2}$ (K*_2-)
etaprime  $\eta ^{\prime }$ (eta')
phi  $\phi $ (phi)
fprime_2  $\mbox{f}^{\prime }_{2}$ (f'_2)
Dplus  $\mbox{D}^{+}$ (D+)
Dminus  $\mbox{D}^{-}$ (D-)
Dstarplus  $\mbox{D}^{*+}$ (D*+)
Dstarminus  $\mbox{D}^{*-}$ (D*-)
Dstar_2plus  $\mbox{D}^{*+}_{2}$ (D*_2+)
Dstar_2minus  $\mbox{D}^{*-}_{2}$ (D*_2-)
D0  $\mbox{D}^{0 }$ (D0)
Dbar0  $\overline{\mbox{D}}^{0 }$ (Dbar0)
Dstar0  $\mbox{D}^{*0 }$ (D*0)
Dstarbar0  $\overline{\mbox{D}}^{*0 }$ (D*bar0)
Dstar_20  $\mbox{D}^{*0 }_{2}$ (D*_20)
Dstar_2bar0  $\overline{\mbox{D}}^{*0 }_{2}$ (D*_2bar0)
D_splus  $\mbox{D}^{+}_{s}$ (D_s+)
D_sminus  $\mbox{D}^{-}_{s}$ (D_s-)
Dstar_splus  $\mbox{D}^{*+}_{s}$ (D*_s+)
Dstar_sminus  $\mbox{D}^{*-}_{s}$ (D*_s-)
Dstar_2splus  $\mbox{D}^{*+}_{2s}$ (D*_2s+)
Dstar_2sminus  $\mbox{D}^{*-}_{2s}$ (D*_2s-)
eta_c  $\eta _{c}$ (eta_c)
Jpsi  $J/\psi $ (J/psi)
chi_2c  $\chi _{2c}$ (chi_2c)
B0  $\mbox{B}^{0 }$ (B0)
Bbar0  $\overline{\mbox{B}}^{0 }$ (Bbar0)
Bstar0  $\mbox{B}^{*0 }$ (B*0)
Bstarbar0  $\overline{\mbox{B}}^{*0 }$ (B*bar0)
Bstar_20  $\mbox{B}^{*0 }_{2}$ (B*_20)
Bstar_2bar0  $\overline{\mbox{B}}^{*0 }_{2}$ (B*_2bar0)
Bplus  $\mbox{B}^{+}$ (B+)
Bminus  $\mbox{B}^{-}$ (B-)
Bstarplus  $\mbox{B}^{*+}$ (B*+)
Bstarminus  $\mbox{B}^{*-}$ (B*-)
Bstar_2plus  $\mbox{B}^{*+}_{2}$ (B*_2+)
Bstar_2minus  $\mbox{B}^{*-}_{2}$ (B*_2-)
B_s0  $\mbox{B}^{0 }_{s}$ (B_s0)
B_sbar0  $\overline{\mbox{B}}^{0 }_{s}$ (B_sbar0)
Bstar_s0  $\mbox{B}^{*0 }_{s}$ (B*_s0)
Bstar_sbar0  $\overline{\mbox{B}}^{*0 }_{s}$ (B*_sbar0)
Bstar_2s0  $\mbox{B}^{*0 }_{2s}$ (B*_2s0)
Bstar_2sbar0  $\overline{\mbox{B}}^{*0 }_{2s}$ (B*_2sbar0)
B_cplus  $\mbox{B}^{+}_{c}$ (B_c+)
B_cminus  $\mbox{B}^{-}_{c}$ (B_c-)
Bstar_cplus  $\mbox{B}^{*+}_{c}$ (B*_c+)
Bstar_cminus  $\mbox{B}^{*-}_{c}$ (B*_c-)
Bstar_2cplus  $\mbox{B}^{*+}_{2c}$ (B*_2c+)
Bstar_2cminus  $\mbox{B}^{*-}_{2c}$ (B*_2c-)
eta_b  $\eta _{b}$ (eta_b)
Upsilon  $\Upsilon $ (Upsilon)
chi_2b  $\chi _{2b}$ (chi_2b)
pomeron  $I\!\!P$ (pomeron)
dd_1  $\mbox{dd}_{1}$ (dd_1)
dd_1bar  $\overline{\mbox{dd}}_{1}$ (dd_1bar)
Deltaminus  $\Delta ^{-}$ (Delta-)
Deltabarplus  $\overline{\Delta }^{+}$ (Deltabar+)
ud_0  $\mbox{ud}^{0 }$ (ud_0)
ud_0bar  $\overline{\mbox{ud}}^{0 }$ (ud_0bar)
ud_1  $\mbox{ud}_{1}$ (ud_1)
ud_1bar  $\overline{\mbox{ud}}_{1}$ (ud_1bar)
n0  $\mbox{n}^{0 }$ (n0)
nbar0  $\overline{\mbox{n}}^{0 }$ (nbar0)
Delta0  $\Delta ^{0 }$ (Delta0)
Deltabar0  $\overline{\Delta }^{0 }$ (Deltabar0)
uu_1  $\mbox{uu}_{1}$ (uu_1)
uu_1bar  $\overline{\mbox{uu}}_{1}$ (uu_1bar)
pplus  $\mbox{p}^{+}$ (p+)
pbarminus  $\overline{\mbox{p}}^{-}$ (pbar-)
Deltaplus  $\Delta ^{+}$ (Delta+)
Deltabarminus  $\overline{\Delta }^{-}$ (Deltabar-)
Deltaplus2  $\Delta ^{++}$ (Delta++)
Deltabarminus2  $\overline{\Delta }^{--}$ (Deltabar--)
sd_0  $\mbox{sd}^{0 }$ (sd_0)
sd_0bar  $\overline{\mbox{sd}}^{0 }$ (sd_0bar)
sd_1  $\mbox{sd}_{1}$ (sd_1)
sd_1bar  $\overline{\mbox{sd}}_{1}$ (sd_1bar)
Sigmaminus  $\Sigma ^{-}$ (Sigma-)
Sigmabarplus  $\overline{\Sigma }^{+}$ (Sigmabar+)
Sigmastarminus  $\Sigma ^{*-}$ (Sigma*-)
Sigmastarbarplus  $\overline{\Sigma }^{*+}$ (Sigma*bar+)
Lambda0  $\Lambda ^{0 }$ (Lambda0)
Lambdabar0  $\overline{\Lambda }^{0 }$ (Lambdabar0)
su_0  $\mbox{su}^{0 }$ (su_0)
su_0bar  $\overline{\mbox{su}}^{0 }$ (su_0bar)
su_1  $\mbox{su}_{1}$ (su_1)
su_1bar  $\overline{\mbox{su}}_{1}$ (su_1bar)
Sigma0  $\Sigma ^{0 }$ (Sigma0)
Sigmabar0  $\overline{\Sigma }^{0 }$ (Sigmabar0)
Sigmastar0  $\Sigma ^{*0 }$ (Sigma*0)
Sigmastarbar0  $\overline{\Sigma }^{*0 }$ (Sigma*bar0)
Sigmaplus  $\Sigma ^{+}$ (Sigma+)
Sigmabarminus  $\overline{\Sigma }^{-}$ (Sigmabar-)
Sigmastarplus  $\Sigma ^{*+}$ (Sigma*+)
Sigmastarbarminus  $\overline{\Sigma }^{*-}$ (Sigma*bar-)
ss_1  $\mbox{ss}_{1}$ (ss_1)
ss_1bar  $\overline{\mbox{ss}}_{1}$ (ss_1bar)
Ximinus  $\Xi ^{-}$ (Xi-)
Xibarplus  $\overline{\Xi }^{+}$ (Xibar+)
Xistarminus  $\Xi ^{*-}$ (Xi*-)
Xistarbarplus  $\overline{\Xi }^{*+}$ (Xi*bar+)
Xi0  $\Xi ^{0 }$ (Xi0)
Xibar0  $\overline{\Xi }^{0 }$ (Xibar0)
Xistar0  $\Xi ^{*0 }$ (Xi*0)
Xistarbar0  $\overline{\Xi }^{*0 }$ (Xi*bar0)
Omegaminus  $\Omega ^{-}$ (Omega-)
Omegabarplus  $\overline{\Omega }^{+}$ (Omegabar+)
cd_0  $\mbox{cd}^{0 }$ (cd_0)
cd_0bar  $\overline{\mbox{cd}}^{0 }$ (cd_0bar)
cd_1  $\mbox{cd}_{1}$ (cd_1)
cd_1bar  $\overline{\mbox{cd}}_{1}$ (cd_1bar)
Sigma_c0  $\Sigma ^{0 }_{c}$ (Sigma_c0)
Sigma_cbar0  $\overline{\Sigma }^{0 }_{c}$ (Sigma_cbar0)
Sigmastar_c0  $\Sigma ^{*0 }_{c}$ (Sigma*_c0)
Sigmastar_cbar0  $\overline{\Sigma }^{*0 }_{c}$ (Sigma*_cbar0)
Lambda_cplus  $\Lambda ^{+}_{c}$ (Lambda_c+)
Lambda_cbarminus  $\overline{\Lambda }^{-}_{c}$ (Lambda_cbar-)
Xi_c0  $\Xi ^{0 }_{c}$ (Xi_c0)
Xi_cbar0  $\overline{\Xi }^{0 }_{c}$ (Xi_cbar0)
cu_0  $\mbox{cu}^{0 }$ (cu_0)
cu_0bar  $\overline{\mbox{cu}}^{0 }$ (cu_0bar)
cu_1  $\mbox{cu}_{1}$ (cu_1)
cu_1bar  $\overline{\mbox{cu}}_{1}$ (cu_1bar)
Sigma_cplus  $\Sigma ^{+}_{c}$ (Sigma_c+)
Sigma_cbarminus  $\overline{\Sigma }^{-}_{c}$ (Sigma_cbar-)
Sigmastar_cplus  $\Sigma ^{*+}_{c}$ (Sigma*_c+)
Sigmastar_cbarminus  $\overline{\Sigma }^{*-}_{c}$ (Sigma*_cbar-)
Sigma_cplus2  $\Sigma ^{++}_{c}$ (Sigma_c++)
Sigma_cbarminus2  $\overline{\Sigma }^{--}_{c}$ (Sigma_cbar--)
Sigmastar_cplus2  $\Sigma ^{*++}_{c}$ (Sigma*_c++)
Sigmastar_cbarminus2  $\overline{\Sigma }^{*--}_{c}$ (Sigma*_cbar--)
Xi_cplus  $\Xi ^{+}_{c}$ (Xi_c+)
Xi_cbarminus  $\overline{\Xi }^{-}_{c}$ (Xi_cbar-)
cs_0  $\mbox{cs}^{0 }$ (cs_0)
cs_0bar  $\overline{\mbox{cs}}^{0 }$ (cs_0bar)
cs_1  $\mbox{cs}_{1}$ (cs_1)
cs_1bar  $\overline{\mbox{cs}}_{1}$ (cs_1bar)
Xiprime_c0  $\Xi ^{\prime 0 }_{c}$ (Xi'_c0)
Xiprime_cbar0  $\overline{\Xi }^{\prime 0 }_{c}$ (Xi'_cbar0)
Xistar_c0  $\Xi ^{*0 }_{c}$ (Xi*_c0)
Xistar_cbar0  $\overline{\Xi }^{*0 }_{c}$ (Xi*_cbar0)
Xiprime_cplus  $\Xi ^{\prime +}_{c}$ (Xi'_c+)
Xiprime_cbarminus  $\overline{\Xi }^{\prime -}_{c}$ (Xi'_cbar-)
Xistar_cplus  $\Xi ^{*+}_{c}$ (Xi*_c+)
Xistar_cbarminus  $\overline{\Xi }^{*-}_{c}$ (Xi*_cbar-)
Omega_c0  $\Omega ^{0 }_{c}$ (Omega_c0)
Omega_cbar0  $\overline{\Omega }^{0 }_{c}$ (Omega_cbar0)
Omegastar_c0  $\Omega ^{*0 }_{c}$ (Omega*_c0)
Omegastar_cbar0  $\overline{\Omega }^{*0 }_{c}$ (Omega*_cbar0)
cc_1  $\mbox{cc}_{1}$ (cc_1)
cc_1bar  $\overline{\mbox{cc}}_{1}$ (cc_1bar)
Xi_ccplus  $\Xi ^{+}_{cc}$ (Xi_cc+)
Xi_ccbarminus  $\overline{\Xi }^{-}_{cc}$ (Xi_ccbar-)
Xistar_ccplus  $\Xi ^{*+}_{cc}$ (Xi*_cc+)
Xistar_ccbarminus  $\overline{\Xi }^{*-}_{cc}$ (Xi*_ccbar-)
Xi_ccplus2  $\Xi ^{++}_{cc}$ (Xi_cc++)
Xi_ccbarminus2  $\overline{\Xi }^{--}_{cc}$ (Xi_ccbar--)
Xistar_ccplus2  $\Xi ^{*++}_{cc}$ (Xi*_cc++)
Xistar_ccbarminus2  $\overline{\Xi }^{*--}_{cc}$ (Xi*_ccbar--)
Omega_ccplus  $\Omega ^{+}_{cc}$ (Omega_cc+)
Omega_ccbarminus  $\overline{\Omega }^{-}_{cc}$ (Omega_ccbar-)
Omegastar_ccplus  $\Omega ^{*+}_{cc}$ (Omega*_cc+)
Omegastar_ccbarminus  $\overline{\Omega }^{*-}_{cc}$ (Omega*_ccbar-)
Omegastar_cccplus2  $\Omega ^{*++}_{ccc}$ (Omega*_ccc++)
Omegastar_cccbarminus  $\overline{\Omega }^{*-}_{ccc}$ (Omega*_cccbar-)
bd_0  $\mbox{bd}^{0 }$ (bd_0)
bd_0bar  $\overline{\mbox{bd}}^{0 }$ (bd_0bar)
bd_1  $\mbox{bd}_{1}$ (bd_1)
bd_1bar  $\overline{\mbox{bd}}_{1}$ (bd_1bar)
Sigma_bminus  $\Sigma ^{-}_{b}$ (Sigma_b-)
Sigma_bbarplus  $\overline{\Sigma }^{+}_{b}$ (Sigma_bbar+)
Sigmastar_bminus  $\Sigma ^{*-}_{b}$ (Sigma*_b-)
Sigmastar_bbarplus  $\overline{\Sigma }^{*+}_{b}$ (Sigma*_bbar+)
Lambda_b0  $\Lambda ^{0 }_{b}$ (Lambda_b0)
Lambda_bbar0  $\overline{\Lambda }^{0 }_{b}$ (Lambda_bbar0)
Xi_bminus  $\Xi ^{-}_{b}$ (Xi_b-)
Xi_bbarplus  $\overline{\Xi }^{+}_{b}$ (Xi_bbar+)
Xi_bc0  $\Xi ^{0 }_{bc}$ (Xi_bc0)
Xi_bcbar0  $\overline{\Xi }^{0 }_{bc}$ (Xi_bcbar0)
bu_0  $\mbox{bu}^{0 }$ (bu_0)
bu_0bar  $\overline{\mbox{bu}}^{0 }$ (bu_0bar)
bu_1  $\mbox{bu}_{1}$ (bu_1)
bu_1bar  $\overline{\mbox{bu}}_{1}$ (bu_1bar)
Sigma_b0  $\Sigma ^{0 }_{b}$ (Sigma_b0)
Sigma_bbar0  $\overline{\Sigma }^{0 }_{b}$ (Sigma_bbar0)
Sigmastar_b0  $\Sigma ^{*0 }_{b}$ (Sigma*_b0)
Sigmastar_bbar0  $\overline{\Sigma }^{*0 }_{b}$ (Sigma*_bbar0)
Sigma_bplus  $\Sigma ^{+}_{b}$ (Sigma_b+)
Sigma_bbarminus  $\overline{\Sigma }^{-}_{b}$ (Sigma_bbar-)
Sigmastar_bplus  $\Sigma ^{*+}_{b}$ (Sigma*_b+)
Sigmastar_bbarminus  $\overline{\Sigma }^{*-}_{b}$ (Sigma*_bbar-)
Xi_b0  $\Xi ^{0 }_{b}$ (Xi_b0)
Xi_bbar0  $\overline{\Xi }^{0 }_{b}$ (Xi_bbar0)
Xi_bcplus  $\Xi ^{+}_{bc}$ (Xi_bc+)
Xi_bcbarminus  $\overline{\Xi }^{-}_{bc}$ (Xi_bcbar-)
bs_0  $\mbox{bs}^{0 }$ (bs_0)
bs_0bar  $\overline{\mbox{bs}}^{0 }$ (bs_0bar)
bs_1  $\mbox{bs}_{1}$ (bs_1)
bs_1bar  $\overline{\mbox{bs}}_{1}$ (bs_1bar)
Xiprime_bminus  $\Xi ^{\prime -}_{b}$ (Xi'_b-)
Xiprime_bbarplus  $\overline{\Xi }^{\prime +}_{b}$ (Xi'_bbar+)
Xistar_bminus  $\Xi ^{*-}_{b}$ (Xi*_b-)
Xistar_bbarplus  $\overline{\Xi }^{*+}_{b}$ (Xi*_bbar+)
Xiprime_b0  $\Xi ^{\prime 0 }_{b}$ (Xi'_b0)
Xiprime_bbar0  $\overline{\Xi }^{\prime 0 }_{b}$ (Xi'_bbar0)
Xistar_b0  $\Xi ^{*0 }_{b}$ (Xi*_b0)
Xistar_bbar0  $\overline{\Xi }^{*0 }_{b}$ (Xi*_bbar0)
Omega_bminus  $\Omega ^{-}_{b}$ (Omega_b-)
Omega_bbarplus  $\overline{\Omega }^{+}_{b}$ (Omega_bbar+)
Omegastar_bminus  $\Omega ^{*-}_{b}$ (Omega*_b-)
Omegastar_bbarplus  $\overline{\Omega }^{*+}_{b}$ (Omega*_bbar+)
Omega_bc0  $\Omega ^{0 }_{bc}$ (Omega_bc0)
Omega_bcbar0  $\overline{\Omega }^{0 }_{bc}$ (Omega_bcbar0)
bc_0  $\mbox{bc}^{0 }$ (bc_0)
bc_0bar  $\overline{\mbox{bc}}^{0 }$ (bc_0bar)
bc_1  $\mbox{bc}_{1}$ (bc_1)
bc_1bar  $\overline{\mbox{bc}}_{1}$ (bc_1bar)
Xiprime_bc0  $\Xi ^{\prime 0 }_{bc}$ (Xi'_bc0)
Xiprime_bcbar0  $\overline{\Xi }^{\prime 0 }_{bc}$ (Xi'_bcbar0)
Xistar_bc0  $\Xi ^{*0 }_{bc}$ (Xi*_bc0)
Xistar_bcbar0  $\overline{\Xi }^{*0 }_{bc}$ (Xi*_bcbar0)
Xiprime_bcplus  $\Xi ^{\prime +}_{bc}$ (Xi'_bc+)
Xiprime_bcbarminus  $\overline{\Xi }^{\prime -}_{bc}$ (Xi'_bcbar-)
Xistar_bcplus  $\Xi ^{*+}_{bc}$ (Xi*_bc+)
Xistar_bcbarminus  $\overline{\Xi }^{*-}_{bc}$ (Xi*_bcbar-)
Omegaprime_bc0  $\Omega ^{\prime 0 }_{bc}$ (Omega'_bc0)
Omegaprime_bcba  $\overline{\Omega }^{\prime }_{bc}$ (Omega'_bcba)
Omegastar_bc0  $\Omega ^{*0 }_{bc}$ (Omega*_bc0)
Omegastar_bcbar0  $\overline{\Omega }^{*0 }_{bc}$ (Omega*_bcbar0)
Omega_bccplus  $\Omega ^{+}_{bcc}$ (Omega_bcc+)
Omega_bccbarminus  $\overline{\Omega }^{-}_{bcc}$ (Omega_bccbar-)
Omegastar_bccplus  $\Omega ^{*+}_{bcc}$ (Omega*_bcc+)
Omegastar_bccbarminus  $\overline{\Omega }^{*-}_{bcc}$ (Omega*_bccbar-)
bb_1  $\mbox{bb}_{1}$ (bb_1)
bb_1bar  $\overline{\mbox{bb}}_{1}$ (bb_1bar)
Xi_bbminus  $\Xi ^{-}_{bb}$ (Xi_bb-)
Xi_bbbarplus  $\overline{\Xi }^{+}_{bb}$ (Xi_bbbar+)
Xistar_bbminus  $\Xi ^{*-}_{bb}$ (Xi*_bb-)
Xistar_bbbarplus  $\overline{\Xi }^{*+}_{bb}$ (Xi*_bbbar+)
Xi_bb0  $\Xi ^{0 }_{bb}$ (Xi_bb0)
Xi_bbbar0  $\overline{\Xi }^{0 }_{bb}$ (Xi_bbbar0)
Xistar_bb0  $\Xi ^{*0 }_{bb}$ (Xi*_bb0)
Xistar_bbbar0  $\overline{\Xi }^{*0 }_{bb}$ (Xi*_bbbar0)
Omega_bbminus  $\Omega ^{-}_{bb}$ (Omega_bb-)
Omega_bbbarplus  $\overline{\Omega }^{+}_{bb}$ (Omega_bbbar+)
Omegastar_bbminus  $\Omega ^{*-}_{bb}$ (Omega*_bb-)
Omegastar_bbbarplus  $\overline{\Omega }^{*+}_{bb}$ (Omega*_bbbar+)
Omega_bbc0  $\Omega ^{0 }_{bbc}$ (Omega_bbc0)
Omega_bbcbar0  $\overline{\Omega }^{0 }_{bbc}$ (Omega_bbcbar0)
Omegastar_bbc0  $\Omega ^{*0 }_{bbc}$ (Omega*_bbc0)
Omegastar_bbcbar0  $\overline{\Omega }^{*0 }_{bbc}$ (Omega*_bbcbar0)
Omegastar_bbbminus  $\Omega ^{*-}_{bbb}$ (Omega*_bbb-)
Omegastar_bbbbarplus  $\overline{\Omega }^{*+}_{bbb}$ (Omega*_bbbbar+)
a_00  $\mbox{a}^{0 }$ (a_00)
b_10  $\mbox{b}^{0 }_{1}$ (b_10)
a_0plus  $\mbox{a}^{0 +}$ (a_0+)
a_0minus  $\mbox{a}^{0 -}$ (a_0-)
b_1plus  $\mbox{b}^{+}_{1}$ (b_1+)
b_1minus  $\mbox{b}^{-}_{1}$ (b_1-)
f_0  $\mbox{f}^{0 }$ (f_0)
h_1  $\mbox{h}_{1}$ (h_1)
Kstar_00  $\mbox{K}^{*0 }$ (K*_00)
Kstar_0bar0  $\overline{\mbox{K}}^{*0 }$ (K*_0bar0)
K_10  $\mbox{K}^{0 }_{1}$ (K_10)
K_1bar0  $\overline{\mbox{K}}^{0 }_{1}$ (K_1bar0)
Kstar_0plus  $\mbox{K}^{*0 +}$ (K*_0+)
Kstar_0minus  $\mbox{K}^{*0 -}$ (K*_0-)
K_1plus  $\mbox{K}^{+}_{1}$ (K_1+)
K_1minus  $\mbox{K}^{-}_{1}$ (K_1-)
eta1440  $\eta ^{0 }_{144}$ (eta1440)
hprime_1  $\mbox{h}^{\prime }_{1}$ (h'_1)
Dstar_0plus  $\mbox{D}^{*0 +}$ (D*_0+)
Dstar_0minus  $\mbox{D}^{*0 -}$ (D*_0-)
D_1plus  $\mbox{D}^{+}_{1}$ (D_1+)
D_1minus  $\mbox{D}^{-}_{1}$ (D_1-)
Dstar_00  $\mbox{D}^{*0 }$ (D*_00)
Dstar_0bar0  $\overline{\mbox{D}}^{*0 }$ (D*_0bar0)
D_10  $\mbox{D}^{0 }_{1}$ (D_10)
D_1bar0  $\overline{\mbox{D}}^{0 }_{1}$ (D_1bar0)
Dstar_0splus  $\mbox{D}^{*+}_{0s}$ (D*_0s+)
Dstar_0sminus  $\mbox{D}^{*-}_{0s}$ (D*_0s-)
D_1splus  $\mbox{D}^{+}_{1s}$ (D_1s+)
D_1sminus  $\mbox{D}^{-}_{1s}$ (D_1s-)
chi_0c  $\chi _{0c}$ (chi_0c)
h_1c  $\mbox{h}_{1c}$ (h_1c)
Bstar_00  $\mbox{B}^{*0 }$ (B*_00)
Bstar_0bar0  $\overline{\mbox{B}}^{*0 }$ (B*_0bar0)
B_10  $\mbox{B}^{0 }_{1}$ (B_10)
B_1bar0  $\overline{\mbox{B}}^{0 }_{1}$ (B_1bar0)
Bstar_0plus  $\mbox{B}^{*0 +}$ (B*_0+)
Bstar_0minus  $\mbox{B}^{*0 -}$ (B*_0-)
B_1plus  $\mbox{B}^{+}_{1}$ (B_1+)
B_1minus  $\mbox{B}^{-}_{1}$ (B_1-)
Bstar_0s0  $\mbox{B}^{*0 }_{0s}$ (B*_0s0)
Bstar_0sbar0  $\overline{\mbox{B}}^{*0 }_{0s}$ (B*_0sbar0)
B_1s0  $\mbox{B}^{0 }_{1s}$ (B_1s0)
B_1sbar0  $\overline{\mbox{B}}^{0 }_{1s}$ (B_1sbar0)
Bstar_0cplus  $\mbox{B}^{*+}_{0c}$ (B*_0c+)
Bstar_0cminus  $\mbox{B}^{*-}_{0c}$ (B*_0c-)
B_1cplus  $\mbox{B}^{+}_{1c}$ (B_1c+)
B_1cminus  $\mbox{B}^{-}_{1c}$ (B_1c-)
chi_0b  $\chi _{0b}$ (chi_0b)
h_1b  $\mbox{h}_{1b}$ (h_1b)
a_10  $\mbox{a}^{0 }_{1}$ (a_10)
a_1plus  $\mbox{a}^{+}_{1}$ (a_1+)
a_1minus  $\mbox{a}^{-}_{1}$ (a_1-)
f_1  $\mbox{f}_{1}$ (f_1)
Kstar_10  $\mbox{K}^{*0 }_{1}$ (K*_10)
Kstar_1bar0  $\overline{\mbox{K}}^{*0 }_{1}$ (K*_1bar0)
Kstar_1plus  $\mbox{K}^{*+}_{1}$ (K*_1+)
Kstar_1minus  $\mbox{K}^{*-}_{1}$ (K*_1-)
fprime_1  $\mbox{f}^{\prime }_{1}$ (f'_1)
Dstar_1plus  $\mbox{D}^{*+}_{1}$ (D*_1+)
Dstar_1minus  $\mbox{D}^{*-}_{1}$ (D*_1-)
Dstar_10  $\mbox{D}^{*0 }_{1}$ (D*_10)
Dstar_1bar0  $\overline{\mbox{D}}^{*0 }_{1}$ (D*_1bar0)
Dstar_1splus  $\mbox{D}^{*+}_{1s}$ (D*_1s+)
Dstar_1sminus  $\mbox{D}^{*-}_{1s}$ (D*_1s-)
chi_1c  $\chi _{1c}$ (chi_1c)
Bstar_10  $\mbox{B}^{*0 }_{1}$ (B*_10)
Bstar_1bar0  $\overline{\mbox{B}}^{*0 }_{1}$ (B*_1bar0)
Bstar_1plus  $\mbox{B}^{*+}_{1}$ (B*_1+)
Bstar_1minus  $\mbox{B}^{*-}_{1}$ (B*_1-)
Bstar_1s0  $\mbox{B}^{*0 }_{1s}$ (B*_1s0)
Bstar_1sbar0  $\overline{\mbox{B}}^{*0 }_{1s}$ (B*_1sbar0)
Bstar_1cplus  $\mbox{B}^{*+}_{1c}$ (B*_1c+)
Bstar_1cminus  $\mbox{B}^{*-}_{1c}$ (B*_1c-)
chi_1b  $\chi _{1b}$ (chi_1b)
psiprime  $\psi ^{\prime }$ (psi')
Upsilonprime  $\Upsilon ^{\prime }$ (Upsilon')
SUSY_d_L  $\tilde{\mbox{d}}_{L}$ (~d_L)
SUSY_d_Lbar  $\tilde{\overline{\mbox{d}}}_{L}$ (~d_Lbar)
SUSY_u_L  $\tilde{\mbox{u}}_{L}$ (~u_L)
SUSY_u_Lbar  $\tilde{\overline{\mbox{u}}}_{L}$ (~u_Lbar)
SUSY_s_L  $\tilde{\mbox{s}}_{L}$ (~s_L)
SUSY_s_Lbar  $\tilde{\overline{\mbox{s}}}_{L}$ (~s_Lbar)
SUSY_c_L  $\tilde{\mbox{c}}_{L}$ (~c_L)
SUSY_c_Lbar  $\tilde{\overline{\mbox{c}}}_{L}$ (~c_Lbar)
SUSY_b_1  $\tilde{\mbox{b}}_{1}$ (~b_1)
SUSY_b_1bar  $\tilde{\overline{\mbox{b}}}_{1}$ (~b_1bar)
SUSY_t_1  $\tilde{\mbox{t}}_{1}$ (~t_1)
SUSY_t_1bar  $\tilde{\overline{\mbox{t}}}_{1}$ (~t_1bar)
SUSY_e_Lminus  $\tilde{\mbox{e}}^{-}_{L}$ (~e_L-)
SUSY_e_Lplus  $\tilde{\mbox{e}}^{+}_{L}$ (~e_L+)
SUSY_nu_eL  $\tilde{\nu }_{eL}$ (~nu_eL)
SUSY_nu_eLbar  $\tilde{\overline{\nu }}_{eL}$ (~nu_eLbar)
SUSY_mu_Lminus  $\tilde{\mu }^{-}_{L}$ (~mu_L-)
SUSY_mu_Lplus  $\tilde{\mu }^{+}_{L}$ (~mu_L+)
SUSY_nu_muL  $\tilde{\nu }_{\mu L}$ (~nu_muL)
SUSY_nu_muLbar  $\tilde{\overline{\nu }}_{\mu L}$ (~nu_muLbar)
SUSY_tau_1minus  $\tilde{\tau }^{-}_{1}$ (~tau_1-)
SUSY_tau_1plus  $\tilde{\tau }^{+}_{1}$ (~tau_1+)
SUSY_nu_tauL  $\tilde{\nu }_{\tau L}$ (~nu_tauL)
SUSY_nu_tauLbar  $\tilde{\overline{\nu }}_{\tau L}$ (~nu_tauLbar)
SUSY_g  $\tilde{\mbox{g}}$ (~g)
SUSY_chi_10  $\tilde{\chi }^{0 }_{1}$ (~chi_10)
SUSY_chi_20  $\tilde{\chi }^{0 }_{2}$ (~chi_20)
SUSY_chi_1plus  $\tilde{\chi }^{+}_{1}$ (~chi_1+)
SUSY_chi_1minus  $\tilde{\chi }^{-}_{1}$ (~chi_1-)
SUSY_chi_30  $\tilde{\chi }^{0 }_{3}$ (~chi_30)
SUSY_chi_40  $\tilde{\chi }^{0 }_{4}$ (~chi_40)
SUSY_chi_2plus  $\tilde{\chi }^{+}_{2}$ (~chi_2+)
SUSY_chi_2minus  $\tilde{\chi }^{-}_{2}$ (~chi_2-)
SUSY_Gravitino  $\tilde{{\cal G}}$ (~Gravitino)
SUSY_d_R  $\tilde{\mbox{d}}_{R}$ (~d_R)
SUSY_d_Rbar  $\tilde{\overline{\mbox{d}}}_{R}$ (~d_Rbar)
SUSY_u_R  $\tilde{\mbox{u}}_{R}$ (~u_R)
SUSY_u_Rbar  $\tilde{\overline{\mbox{u}}}_{R}$ (~u_Rbar)
SUSY_s_R  $\tilde{\mbox{s}}_{R}$ (~s_R)
SUSY_s_Rbar  $\tilde{\overline{\mbox{s}}}_{R}$ (~s_Rbar)
SUSY_c_R  $\tilde{\mbox{c}}_{R}$ (~c_R)
SUSY_c_Rbar  $\tilde{\overline{\mbox{c}}}_{R}$ (~c_Rbar)
SUSY_b_2  $\tilde{\mbox{b}}_{2}$ (~b_2)
SUSY_b_2bar  $\tilde{\overline{\mbox{b}}}_{2}$ (~b_2bar)
SUSY_t_2  $\tilde{\mbox{t}}_{2}$ (~t_2)
SUSY_t_2bar  $\tilde{\overline{\mbox{t}}}_{2}$ (~t_2bar)
SUSY_e_Rminus  $\tilde{\mbox{e}}^{-}_{R}$ (~e_R-)
SUSY_e_Rplus  $\tilde{\mbox{e}}^{+}_{R}$ (~e_R+)
SUSY_nu_eR  $\tilde{\nu }_{eR}$ (~nu_eR)
SUSY_nu_eRbar  $\tilde{\overline{\nu }}_{eR}$ (~nu_eRbar)
SUSY_mu_Rminus  $\tilde{\mu }^{-}_{R}$ (~mu_R-)
SUSY_mu_Rplus  $\tilde{\mu }^{+}_{R}$ (~mu_R+)
SUSY_nu_muR  $\tilde{\nu }_{\mu R}$ (~nu_muR)
SUSY_nu_muRbar  $\tilde{\overline{\nu }}_{\mu R}$ (~nu_muRbar)
SUSY_tau_2minus  $\tilde{\tau }^{-}_{2}$ (~tau_2-)
SUSY_tau_2plus  $\tilde{\tau }^{+}_{2}$ (~tau_2+)
SUSY_nu_tauR  $\tilde{\nu }_{\tau R}$ (~nu_tauR)
SUSY_nu_tauRbar  $\tilde{\overline{\nu }}_{\tau R}$ (~nu_tauRbar)
pi_tc0  $\pi ^{0 }_{tc}$ (pi_tc0)
pi_tcplus  $\pi ^{+}_{tc}$ (pi_tc+)
pi_tcminus  $\pi ^{-}_{tc}$ (pi_tc-)
piprime_tc0  $\pi ^{\prime 0 }_{tc}$ (pi'_tc0)
eta_tc0  $\eta ^{0 }_{tc}$ (eta_tc0)
rho_tc0  $\rho ^{0 }_{tc}$ (rho_tc0)
rho_tcplus  $\rho ^{+}_{tc}$ (rho_tc+)
rho_tcminus  $\rho ^{-}_{tc}$ (rho_tc-)
omega_tc  $\omega _{tc}$ (omega_tc)
V8_tc  $\mbox{V}_{8tc}$ (V8_tc)
pi_22_1_tc  $\pi _{22}$ (pi_22_1_tc)
pi_22_8_tc  $\pi _{22}$ (pi_22_8_tc)
rho_11_tc  $\rho _{11}$ (rho_11_tc)
rho_12_tc  $\rho _{12}$ (rho_12_tc)
rho_21_tc  $\rho _{21}$ (rho_21_tc)
rho_22_tc  $\rho _{22}$ (rho_22_tc)
dstar  $\mbox{d}^{*}$ (d*)
dstarbar  $\overline{\mbox{d}}^{*}$ (d*bar)
ustar  $\mbox{u}^{*}$ (u*)
ustarbar  $\overline{\mbox{u}}^{*}$ (u*bar)
estarminus  $\mbox{e}^{*-}$ (e*-)
estarbarplus  $\overline{\mbox{e}}^{*+}$ (e*bar+)
nustar_e0  $\nu ^{*0 }_{e}$ (nu*_e0)
nustar_ebar0  $\overline{\nu }^{*0 }_{e}$ (nu*_ebar0)
Gravitonstar  ${\cal G}^{*}$ (Graviton*)
nu_Re  $\nu _{Re}$ (nu_Re)
nu_Rmu  $\nu _{R\mu }$ (nu_Rmu)
nu_Rtau  $\nu _{R\tau }$ (nu_Rtau)
Z_R0  $\mbox{Z}^{0 }_{R}$ (Z_R0)
W_Rplus  $\mbox{W}^{+}_{R}$ (W_R+)
W_Rminus  $\mbox{W}^{-}_{R}$ (W_R-)
H_Lplus2  $\mbox{H}^{++}_{L}$ (H_L++)
H_Lminus2  $\mbox{H}^{--}_{L}$ (H_L--)
H_Rplus2  $\mbox{H}^{++}_{R}$ (H_R++)
H_Rminus2  $\mbox{H}^{--}_{R}$ (H_R--)
rho_diff0  $\rho ^{0 }_{\mbox{\scriptsize diffr}}$ (rho_diff0)
pi_diffrplus  $\pi ^{+}_{\mbox{\scriptsize diffr}}$ (pi_diffr+)
pi_diffrminus  $\pi ^{-}_{\mbox{\scriptsize diffr}}$ (pi_diffr-)
omega_di  $\omega _{\mbox{\scriptsize diffr}}$ (omega_di)
phi_diff  $\phi _{\mbox{\scriptsize diffr}}$ (phi_diff)
Jpsi_di  $J/\psi _{\mbox{\scriptsize diffr}}$ (J/psi_di)
n_diffr0  $\mbox{n}^{0 }_{\mbox{\scriptsize diffr}}$ (n_diffr0)
n_diffrbar0  $\overline{\mbox{n}}^{0 }_{\mbox{\scriptsize diffr}}$ (n_diffrbar0)
p_diffrplus  $\mbox{p}^{+}_{\mbox{\scriptsize diffr}}$ (p_diffr+)
p_diffrbarminus  $\overline{\mbox{p}}^{-}_{\mbox{\scriptsize diffr}}$ (p_diffrbar-)
undefined  Undefined particle.

Definition at line 23 of file EnumParticles.h.

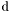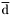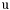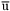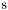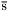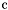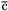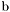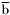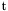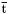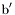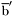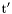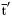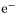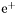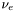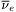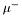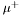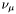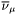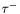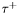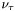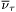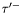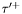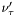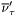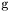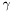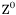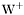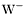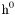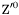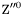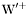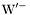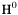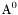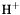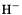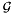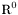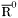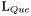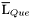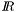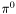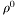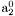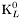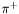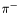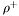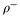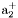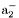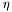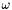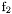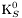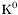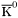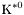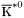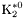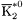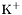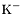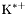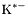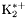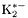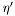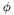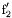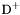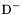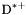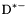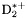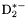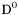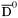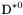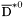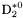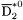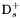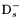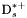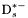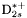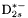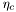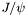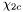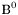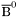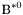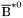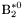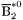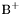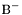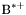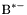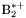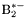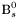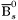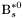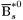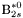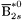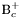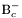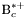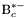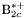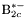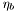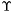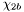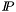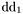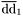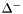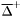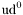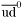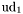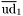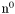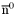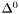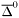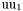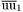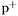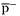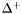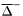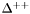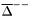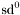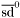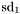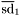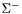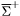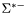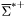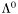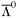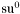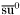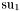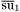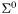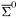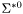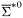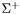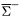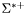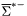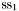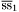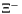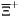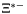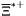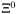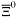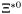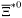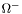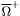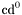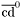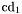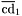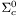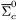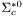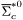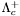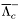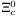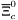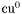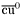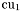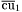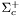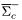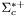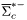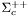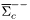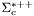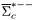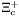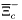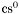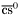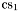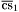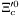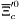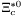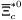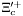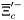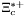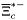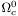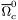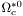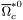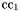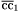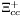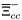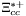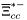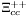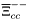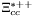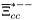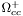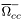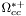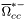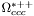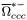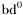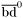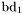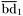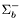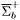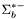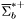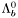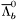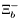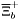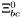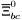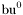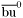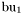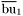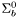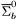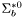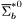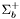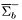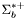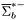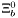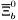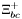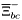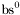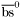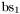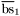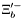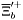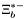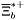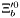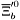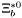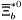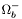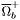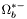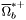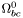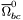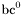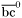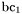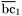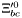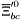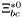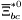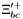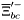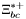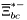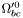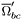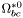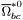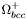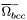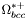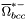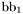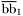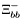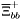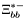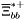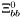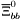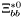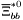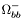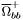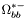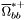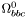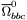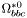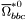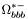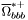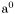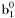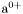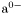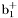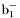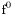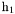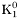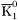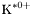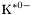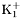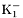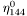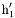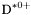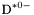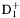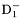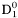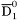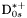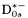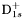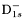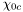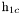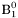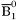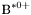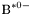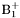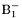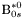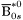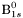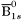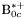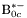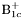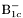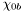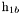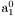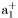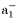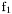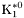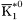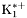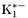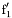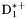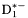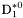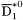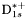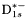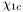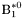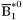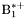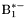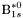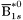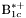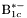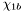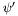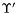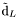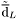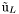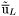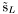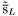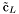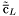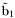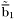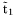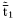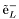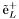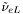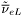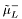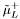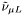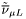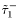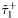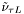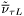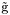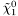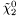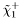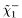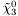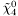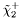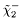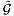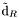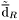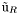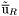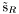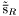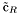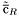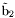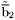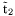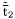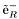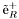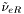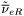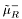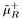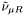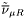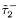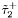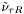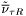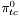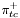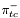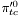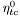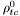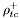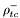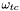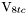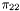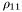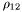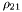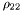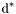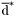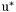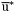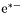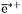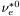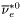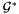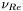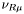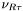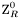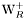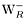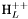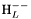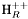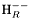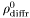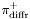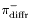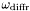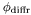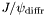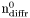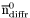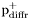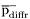Generated on Thu Apr 29 12:43:33 2010 for ThePEG by  doxygen 1.5.5