linear regression.
More...
#include <yat/regression/LinearWeighted.h>
| double theplu::yat::regression::LinearWeighted::alpha |
( |
void |
| ) |
const |
| double theplu::yat::regression::LinearWeighted::alpha_var |
( |
void |
| ) |
const |
Variance is estimated as 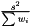
- See Also
- s2()
- Returns
- variance of parameter
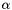
| double theplu::yat::regression::LinearWeighted::beta |
( |
void |
| ) |
const |
| double theplu::yat::regression::LinearWeighted::beta_var |
( |
void |
| ) |
const |
Variance is estimated as 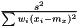
- See Also
- s2()
- Returns
- variance of parameter
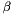
| double theplu::yat::regression::LinearWeighted::predict |
( |
const double |
x | ) |
const |
|
virtual |
| double theplu::yat::regression::OneDimensionalWeighted::prediction_error2 |
( |
const double |
x, |
|
|
const double |
w = 1.0 |
|
) |
| const |
|
inherited |
| double theplu::yat::regression::OneDimensionalWeighted::r2 |
( |
void |
| ) |
const |
|
inherited |
r2 is defined as 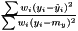 or the fraction of the variance explained by the regression model.
or the fraction of the variance explained by the regression model.
| double theplu::yat::regression::LinearWeighted::s2 |
( |
double |
w = 1 | ) |
const |
|
virtual |
| double theplu::yat::regression::LinearWeighted::standard_error2 |
( |
const double |
x | ) |
const |
|
virtual |
Averager for pair of x and y
| double theplu::yat::regression::OneDimensionalWeighted::chisq_ |
|
protectedinherited |
Chi-squared.
Chi-squared is defined as the 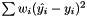
The documentation for this class was generated from the following file:

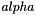 is estimated as
is estimated as 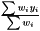
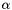
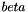 is estimated as
is estimated as 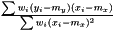
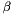
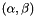 of the model
of the model 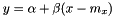 from vectors x and y, by minimizing
from vectors x and y, by minimizing 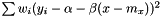 , where
, where 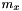 is the weighted average. By construction
is the weighted average. By construction 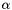 and
and 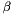 are independent.
are independent. 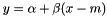
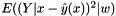 and is typically divided into the conditional variance ( see s2() ) given
and is typically divided into the conditional variance ( see s2() ) given 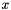 and the squared standard error ( see standard_error2() ) of the model estimation in
and the squared standard error ( see standard_error2() ) of the model estimation in 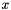 .
.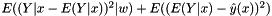
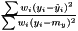 or the fraction of the variance explained by the regression model.
or the fraction of the variance explained by the regression model. 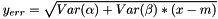 .
. 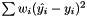
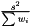
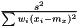
 1.8.5
1.8.5