Interface Class for One Dimensional fitting in a weighted fashion. More...
#include <yat/regression/OneDimensionalWeighted.h>

Public Member Functions | |
| OneDimensionalWeighted (void) | |
| virtual | ~OneDimensionalWeighted (void) |
| virtual void | fit (const utility::VectorBase &x, const utility::VectorBase &y, const utility::VectorBase &w)=0 |
| virtual double | predict (const double x) const =0 |
| double | prediction_error2 (const double x, const double w=1.0) const |
| double | r2 (void) const |
| virtual double | s2 (double w=1) const =0 |
| virtual double | standard_error2 (const double x) const =0 |
Protected Attributes | |
| statistics::AveragerPairWeighted | ap_ |
| double | chisq_ |
| Chi-squared. More... | |
Detailed Description
Interface Class for One Dimensional fitting in a weighted fashion.
Constructor & Destructor Documentation
| theplu::yat::regression::OneDimensionalWeighted::OneDimensionalWeighted | ( | void | ) |
Default Constructor.
|
virtual |
Destructor
Member Function Documentation
|
pure virtual |
This function computes the best-fit given a model (see specific class for details) by minimizing 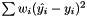 , where
, where 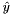 is the fitted value. The weight
is the fitted value. The weight 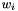 should be proportional to the inverse of the variance for
should be proportional to the inverse of the variance for 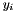
Implemented in theplu::yat::regression::LinearWeighted, theplu::yat::regression::NaiveWeighted, and theplu::yat::regression::PolynomialWeighted.
|
pure virtual |
- Returns
- expected value in x according to the fitted model
Implemented in theplu::yat::regression::LinearWeighted, theplu::yat::regression::PolynomialWeighted, and theplu::yat::regression::NaiveWeighted.
| double theplu::yat::regression::OneDimensionalWeighted::prediction_error2 | ( | const double | x, |
| const double | w = 1.0 |
||
| ) | const |
The prediction error is defined as expected squared deviation a new data point (with weight w) will be from the model value 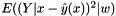 and is typically divided into the conditional variance ( see s2() ) given
and is typically divided into the conditional variance ( see s2() ) given  and the squared standard error ( see standard_error2() ) of the model estimation in
and the squared standard error ( see standard_error2() ) of the model estimation in 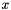 .
.
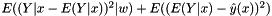
- Returns
- expected prediction error for a new data point in x with weight w.
| double theplu::yat::regression::OneDimensionalWeighted::r2 | ( | void | ) | const |
r2 is defined as 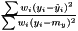 or the fraction of the variance explained by the regression model.
or the fraction of the variance explained by the regression model.
|
pure virtual |
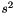 is the estimation of variance of residuals or equivalently the conditional variance of Y.
is the estimation of variance of residuals or equivalently the conditional variance of Y.
- Returns
- Conditional variance of Y
Implemented in theplu::yat::regression::LinearWeighted, theplu::yat::regression::NaiveWeighted, and theplu::yat::regression::PolynomialWeighted.
|
pure virtual |
The standard error is defined as 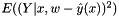
- Returns
- error of model value in x
Implemented in theplu::yat::regression::LinearWeighted, theplu::yat::regression::NaiveWeighted, and theplu::yat::regression::PolynomialWeighted.
Member Data Documentation
|
protected |
Averager for pair of x and y
|
protected |
Chi-squared.
Chi-squared is defined as the 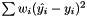
The documentation for this class was generated from the following file:
- yat/regression/OneDimensionalWeighted.h
 1.8.5
1.8.5